Calculando el valor de π

El que la constante que mide la relación entre la longitud de una circunferencia y su diámetro se conozca como número π, y se escriba así, en notación griega, es "relativamente" moderno. Del siglo XVII en concreto, aunque fue Leonhard Euler, en su obra "Introducción al cálculo infinitesimal", de 1748, el que la popularizó (de hecho, proviene de la primera letra de la palabra περίμετρον, que significa perímetro). 

Por supuesto que egipcios y babilónicos conocían esta "curiosidad", que la proporción entre la longitud de una circunferencia y su diámetro era una constante, y que valía "3 y pico". Pero no sabemos cómo la llamaban. Se sabe que en tiempos de Pitágoras (siglo VI a.C.) se tomaba como bueno el valor de π = 3,14, y que tuvieron que pasar muchos años hasta que se desarrolló el método para añadir unas cuantas cifras decimales más. Hoy (desde el siglo XVIII) sabemos que π es lo que se llama un número "irracional", o sea que tiene infinitas cifras decimales no periódicas. Y hay algoritmos que permiten calcular hasta billones de esas cifras...

Pero, como con el rollo de los cierres perimetrales (mira por donde vuelve a salir el perímetro) tenemos tiempo para entretenernos, vamos a ver si, mediante cálculos sencillos, somos capaces de ir acotando el valor de π. Espero que no se me aburran los ilustres ingenieros y científicos seguidores de este blog, ni se desanimen los de letras...

Imaginemos al primer babilonio, por decir algo, que se planteó calcular la longitud de una circunferencia. Lo más sencillo (ver gráfico adjunto) era ver que esa longitud estaría comprendida entre la longitud de un cuadrado inscrito y la de otro cuadrado circunscrito en dicha circunferencia. La longitud del cuadrado circunscrito, de lado L, es fácil de saber: 4L. Y como L=2r, pues la longitud del cuadrado es 8r, y por tanto la de la circunferencia debe ser menor. Hasta ahí, fácil.

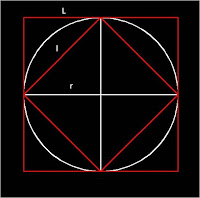
Para calcular la longitud del cuadrado inscrito tenemos que pedir ayuda al Teorema de Pitágoras (sí, ya sé que el babilonio no lo conocería por ese nombre, pero es bastante seguro que sabría que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los catetos). O sea que, en el gráfico: l2 = r2 + r2 = 2r2 (como este editor de textos no me deja, o no sé cómo hacerlo, estos 2´s representan exponentes). Y, por tanto l = r√2. Y la longitud del cuadrado inscrito sería 4l = 4r√2. 

¿Y π? Pues si sabemos que π=C/D (siendo C la longitud de la circunferencia y D=2r su diámetro), lo que nos dicen los cálculos anteriores es que  π es menor que 8r/2r = 4 y mayor que 4r√2/2r = 2√2 = 2,82. O sea, que está comprendido entre 2,82 y 4,0. Pues vaya, para ese viaje... 

Pero el babilonio era persistente y pensó... ¿y si, en lugar de con cuadrados, hago los mismos cálculos con hexágonos, que se ajustarán mejor a la circunferencia? Dicho y hecho...

Utilizando la notación de esta imagen que he pillado por la red, vamos al lío. La longitud del hexágono inscrito es muy fácil de calcular, porque siempre el lado del hexágono inscrito es igual al radio del círculo(r). Por lo tanto, su longitud es 6r, y el π resultante sería 6r/2r= 3,0. Bien, vamos acotando por abajo.

El lado del hexágono circunscrito sería 2x en el dibujo. Y, volviendo a Pitágoras, tendríamos que x2+r2=OB´2. La "a" en el dibujo es la "apotema" del polígono y también a2+(r/2)2=r2, por lo que, resolviendo, da a=(r√3)/2. 

Aplicando la ley de segmentos proporcionales, llegaremos a que OB´= 2r/√3. 

Luego x=r/√3  y la longitud, 6*2x=12x=12r/√3  . Y el valor de π=6/√3  = 3,46. O sea que ya tenemos 3,0 < π < 3,46

Y pensó el babilonio... ¿Y si, en lugar de cuadrados y hexágonos, voy considerando polígonos de 8, 16, 32, 64, 256... lados, cada vez más coincidentes con el perímetro de la circunferencia, y aplico el mismo procedimiento? Pues quizá lo pensó, pero no lo llevó a cabo. Hubo que esperar al matemático chino Liu Hui para que, en el año 263 d.C., realizara este cálculo con un polígono de ¡¡¡3.072 lados!!! y llegara a la cifra de π= 3,14159 que es la que muchos nos aprendimos en el colegio.

(Durante muchos años, la mejor aproximación al valor de π la dio Arquímedes de Siracusa, quien,  hacia el 250 a.C., llegó a determinar, parece que llegando a analizar un polígono de 92 lados, que π estaba comprendido entre 3+10/71 y 3+1/7, que, usando la calculadora, da entre 3,1408 y 3,1428, bastante acotado, la verdad.

Como sucede muchas veces en Matemáticas, la clave para facilitar un cálculo de estas características es encontrar una fórmula "recurrente", es decir, que permita calcular el siguiente valor de una serie en función del que ya se tiene. En el caso de los polígonos cuyo lado se va doblando, esta fórmula es la siguiente:

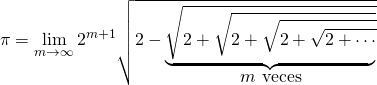
Por ejemplo, para m=1, que sería el perímetro del octógono, el valor es 3,06...; para m=2, el polígono de 16 lados -> 3,12...; para m=3 -> 3,1365 y así sucesivamente).  

Y, para terminar el post, si es que he conseguido que llegues hasta aquí, no me resisto a escribir la demostración más sencilla y gráfica del Teorema de Pitágoras. 

Sólamente hay que construir la figura del gráfico:

Es fácil ver que los cuatro triángulos de colores son iguales, y que su área es (a*b)/2 por lo que, igualando áreas (recuerda que los 2´s detrás de la letra son exponentes):

(a+b)2=c2+4*(a*b)/2) = c2+2ab

a2+b2+2ab=c2+2ab => a2+b2=c2 

(Que yo creo que, visto lo fácil que es llegar a la solución, ya debía de ser conocida por egipcios y mesopotámicos mucho antes de Pitágoras; el por qué se ha quedado el de Samos con la "autoría" del teorema... pues vaya Ud a saber).

_____________________________________________________________

El "inductor" de este post (aunque él no lo sepa) ha sido Marcos Chicot (Madrid, 1971) y su libro "El asesinato de Pitágoras" (Editorial Duomo, 2013) que he leído días atrás. Aunque se trata de una ficción novelada, no deja de tener elementos históricos interesantes y propuestas para despertar la curiosidad del lector, como ha sido en mi caso. 

Por ejemplo, descubrir los pocos datos históricos verdaderamente contrastados que se conocen sobre Pitágoras (c. 569 a.C. - Samos, c. 475 a.C. - Metaponto), hasta el punto de que se puede llegar a dudar de su existencia. Y que la palabra "matemáticas" puede venir por extensión de los discípulos pitagóricos que él llamaba "matematicós" ( μαθηματικοί  - los que poseen cualidades lógicas para aprender), frente a los "acusmaticós" ( ακούσματικοί - los que escuchan las lecciones). Siendo las matemáticas el conjunto de las enseñanzas que luego, en Roma, se conocieron como "cuadrivium": Aritmética, Geometría, Música y una combinación de Astronomía/Astrología.

Y, también, conocer la Magna Grecia, la gran zona del sur de la Península Itálica y de Sicilia que, durante casi 5 siglos, fue parte de Grecia, y donde Pitágoras desarrolló su famosa escuela.

____________________________________________________________________