El que la constante que mide la relación entre la longitud de una circunferencia y su diámetro se conozca como número π, y se escriba así, en notación griega, es "relativamente" moderno. Del siglo XVII en concreto, aunque fue Leonhard Euler, en su obra "Introducción al cálculo infinitesimal", de 1748, el que la popularizó (de hecho, proviene de la primera letra de la palabra περίμετρον, que significa perímetro).
Por supuesto que egipcios y babilónicos conocían esta "curiosidad", que la proporción entre la longitud de una circunferencia y su diámetro era una constante, y que valía "3 y pico". Pero no sabemos cómo la llamaban. Se sabe que en tiempos de Pitágoras (siglo VI a.C.) se tomaba como bueno el valor de π = 3,14, y que tuvieron que pasar muchos años hasta que se desarrolló el método para añadir unas cuantas cifras decimales más. Hoy (desde el siglo XVIII) sabemos que π es lo que se llama un número "irracional", o sea que tiene infinitas cifras decimales no periódicas. Y hay algoritmos que permiten calcular hasta billones de esas cifras...
Pero, como con el rollo de los cierres perimetrales (mira por donde vuelve a salir el perímetro) tenemos tiempo para entretenernos, vamos a ver si, mediante cálculos sencillos, somos capaces de ir acotando el valor de π. Espero que no se me aburran los ilustres ingenieros y científicos seguidores de este blog, ni se desanimen los de letras...
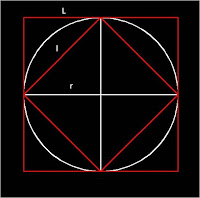
Imaginemos al primer babilonio, por decir algo, que se planteó calcular la longitud de una circunferencia. Lo más sencillo (ver gráfico adjunto) era ver que esa longitud estaría comprendida entre la longitud de un cuadrado inscrito y la de otro cuadrado circunscrito en dicha circunferencia. La longitud del cuadrado circunscrito, de lado L, es fácil de saber: 4L. Y como L=2r, pues la longitud del cuadrado es 8r, y por tanto la de la circunferencia debe ser menor. Hasta ahí, fácil.
Para calcular la longitud del cuadrado inscrito tenemos que pedir ayuda al Teorema de Pitágoras (sí, ya sé que el babilonio no lo conocería por ese nombre, pero es bastante seguro que sabría que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los catetos). O sea que, en el gráfico: l2 = r2 + r2 = 2r2 (como este editor de textos no me deja, o no sé cómo hacerlo, estos 2´s representan exponentes). Y, por tanto l = r√2. Y la longitud del cuadrado inscrito sería 4l = 4r√2.
¿Y π? Pues si sabemos que π=C/D (siendo C la longitud de la circunferencia y D=2r su diámetro), lo que nos dicen los cálculos anteriores es que π es menor que 8r/2r = 4 y mayor que 4r√2/2r = 2√2 = 2,82. O sea, que está comprendido entre 2,82 y 4,0. Pues vaya, para ese viaje...