Sangakus

Tengo que reconocer que, antes del 20 de septiembre, yo no había oído hablar de los sangakus... Fue a raíz de una charla en el "Naukas 2024" de Bilbao, impartida por el matemático profesor en la Universidad del País Vasco, Raúl Ibañez Torres, titulada "Sangakus, pasión por los desafíos matemáticos", cuando me enteré de lo que eran y de su origen, y se despertó mi curiosidad. Con lo que se expuso en la charla y mi "investigación" particular, he escrito lo que viene a continuación, que espero te resulte curioso e interesante, como lo ha sido para mí. (Puedes ver la charla completa, son 10 minutos, aquí). 

Para empezar, hay que aclarar que, aunque fonéticamente suenen parecidos y tengan en común algo de matemáticas, los sangakus y los sudokus son cosas muy diferentes. La traducción de sangaku sería "tablilla matemática", porque eran tablillas como las que se usaban, y se siguen usando, en los templos sintoístas y budistas como ofrenda a las divinidades o seres espirituales (kami). Pero eran unas tablillas especiales: en ellas se plasmaban problemas o desafíos matemáticos con los que también se buscaba el favor de los dioses pero, a la vez, planteaban un reto al resto de los visitantes.

Se entiende mejor con un ejemplo:

Este sangaku propone el siguiente problema (no es que yo sepa japonés, es que lo he encontrado traducido):

Sean 2 sectores circulares de forma que el radio del sector exterior sea el doble del del sector interior. Se inscriben, como se ve en la figura, los 7 círculos tangentes entre ellos y con el exterior. 

El problema consiste en encontrar la razón entre el radio de los círculos pequeños de color rojo y el radio de los círculos de color blanco. 

La solución, no me preguntes cómo se llega a ella, es muy elegante: Si R es el radio de los círculos blancos y r el de los rojos,  R= r (31/2 - 8 ) o, lo que es lo mismo, R= r * 1,6435935... Lo bonito de la solución es que este ratio se cumple para cualquier tamaño del "abanico", siempre que se cumplan las reglas de construcción de la figura.

Los sangakus son una manifestación de lo que más ampliamente se conoce como  和算 wasan , o matemática japonesa, que corresponde a un período de casi 300 años de la historia de Japón en que los nuevos dirigentes del país decidieron cortar relaciones con los demás países y tanto las artes como las ciencias tuvieron un desarrollo aislado, independiente de lo que se hacía en otras partes del mundo. 

Se conoce como período Edo. Duró de 1603 a 1867, coincidiendo con el Shogunato Tokugawa. Al comienzo, tuvo mucho que ver con la decisión de erradicar el cristianismo, que había arraigado con fuerza gracias al trabajo de los misioneros franciscanos a finales del siglo XVI.

Ieyasu Tokugawa, primer sogún de la Dinastía

Copio de la Wikipedia: "En torno al 1600, existían entre setecientos y setecientos cincuenta mil cristianos en Japón. Los Tokugawa y sus partidarios tenían a la nueva religión por un factor desestabilizador que podía llegar a amenazar su poder, en especial en liga con los restos de los seguidores de los Toyotomi. En 1612, a los sirvientes del sogún y a los residentes de las tierras de Tokugawa se les ordenó que renegaran del cristianismo.​ En los feudos Tokugawa se derruyeron los templos cristianos y se prohibió la predicación.​ Más restricciones se dieron a conocer a partir del año siguiente,​ entre ellas la limitación de comercio con extranjeros en Nagasaki y en Hirado. En 1622 se ejecutó a ciento veinte misioneros y conversos.​ En 1624 se expulsó a los españoles y se rompieron las relaciones diplomáticas entre Japón y España.​ En 1629 se ajustició a cientos de cristianos. Se obligó a la población a registrarse en los templos budistas, que se transformaron en oficinas de registro oficiosas.​ Ante la imposibilidad de perseguir el cristianismo y mantener el comercio exterior, el Gobierno optó por sacrificar éste en tiempos del tercer sogún.​ Mediante una serie de decretos emitidos entre 1633 y 1639, el país se aisló del exterior. Finalmente, en 1635, se prohibió que cualquier japonés viajara al extranjero y se dispuso que, si llegaban a salir del país, jamás volvieran.​ Los que se habían asentado en el exterior tenían prohibido el regreso al país. Los portugueses y mestizos fueron asimismo expulsados del imperio".

El caso, para lo que nos ocupa, es que el desarrollo de las matemáticas en Japón en esos siglos siguió un proceso independiente del del resto del mundo. Mientras que, en Europa, Descartes, Newton, Leibniz y compañía se ganaban su buena fama, en Japón eran desconocidos (para nosotros) como  Yoshida Shichibei Kōyū, Imamura Chishō, y Takahara Kisshu, conocidos como "los tres aritméticos", los que posibilitaban el desarrollo de las nuevas matemáticas. 

Copio y traduzco de la Wikipedia inglesa: 

"Yoshida fue el autor del texto matemático japonés más antiguo que se conserva, la obra de 1627 llamada Jinkōki. La obra trataba el tema de la aritmética soroban (basada en el uso del ábaco), incluidas las operaciones de raíz cuadrada y cúbica. El libro de Yoshida inspiró significativamente a una nueva generación de matemáticos y redefinió la percepción japonesa de la iluminación educativa, que se definió en la Constitución de Diecisiete Artículos como "el producto de la meditación seria".

Seki Takakazu fundó Enri: "principio del círculo", un sistema matemático con el mismo propósito que el cálculo, en un momento similar al desarrollo del cálculo en Europa. Sin embargo, las investigaciones de Seki no procedieron de las mismas bases que las utilizadas en los estudios de Newton en Europa.

Matemáticos como Takebe Katahiro desempeñaron un papel importante en el desarrollo de Enri, un análogo del cálculo occidental. Obtuvo la expansión en serie de potencias de (arcsin (x))E2  en 1722, 15 años antes que Euler. Utilizó la extrapolación de Richardson en 1695, unos 200 años antes que Richardson. También calculó 41 dígitos de π, basándose en la aproximación poligonal y la extrapolación de Richardson".

Página del Shinpeki Sanpō - 1789

Volviendo a los sangakus, la tablilla más antigua que se conoce proviene de la prefectura de Tochigi y se remonta a 1683. Aunque, en el diario del matemático Kazu Yamagushi, se alude a una tablilla del año 1668, perdida en la actualidad. De las 2625 tablillas que se supone existieron, se conservan 884. 

Fujita Kagen (1765-1821), matemático japonés, publicó la primera colección de problemas sangaku en sus obras "Shinpeki Sanpō" (Problemas matemáticos suspendidos en el Templo) en 1789, y una segunda parte en 1806, "Zoku Shinpeki Sanpō".

Para ilustrar que la solución de los sangakus puede ser relativamente fácil, aunque imaginativa, os propongo éste (que es una versión de lo que se conoce como el teorema de los círculos de Descartes). Se presentó en la Prefectura de Gunma en 1824.

Son tres circunferencias tangentes entre sí y a una misma recta. Se pide determinar el radio de la circunferencia más pequeña en términos de las dos circunferencias restantes.

Solución: (que no se me desanimen los de letras; es un poco de lógica y teorema de Pitágoras)

Sean las longitudes de los segmentos

O2O3=r2+r3 ,
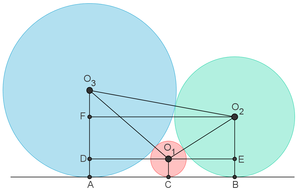
O1O2=r1+r2 y
O1O3=r1+r3 ,que conectan los centros de las circunferencias.

Luego, los segmentos AB y FO2 tienen igual longitud y por Teorema de Pitágoras :

; 

de forma análoga para los segmentos 

 

y 

.
Como AB=AC+CB, tenemos que: 

dividiendo por a ambos lados de la ecuación se llega a la solución:


o

Y, para terminar, os propongo un sangaku fácil (el que propuso Raúl Ibañez al final de su charla): 

Gallifante de premio al primero que aporte la solución correcta (y cómo se ha llegado a ella). Como es difícil escribir fórmulas en los comentarios, podéis enviarme la solución a mi dirección de mail: angeldiazmiguel@hotmail.com

__________________________________________________

Página del Zoku Shinpeki Sanpō - 1806